PENGANTAR
Geoid disebut sebagai model bumi yang mendekati sesungguhnya. Lebih jauh geoid didefinisikan sebagai bidang equipotensial gayaberat atau bidang nivo yang berimpit dengan permukaan laut rata-rata (tidak terganggu) [Kahar, S. 2007 dalam Rastawira, T. 2013]. Di dalam geodesi geoid bereferensi terhadap ellipsoid karena ellipsoid merupakan model matematis pendekatan bumi. Jarak antara permukaan ellipsoid dengan permukaan geoid dinamakan undulasi geoid.
Di dalam geodesi besaran tinggi adalah salah satu unsur posisi yang sangat penting. Geoid merupakan referensi tinggi yang dipakai pada penentuan tinggi orthometrik. Tinggi orthometrik adalah tinggi yang mengacu pada permukaan geoid. Tinggi orthometrik ini lah yang biasa dipakai untuk keperluan praktis seperti rekayasa, survei, dan pemetaan. Pada saat ini dan yang akan datang kebutuhan akan model geoid akan mendesak karena pesatnya pemakaian GPS untuk keperluan rekayasa dan survei pemetaan.
Berdasarkan bidang referensi yang digunakan, dikenal sistem tinggi geodesi geometric dan sistem tinggi geodesi fisis.Terdapat macam macam tinggi fisis yaitu tinggi dinamik, tinggi orthomatrik, dan tinggi normal Navratial dan unger, 2013 dalam Rakapuri, G.,dkk. 2016). Survei pemetaan dan rekayasa dapat menggunakan tinggi geometrik dan tinggi orthometrik yang masing – masing menggunakan bidang referensi berupa ellipsoid dan geoid. Namun demikian, untuk keperluan praktis penentuan tinggi dapat menggunakan bidang referensi berupa mean sea level (MSL).MSL direalisaikan dengan tanda titik geodesi (TTG). Indonesia yang terdiri dari berbagai pulau tidak memungkinkan di bentuknya jaring TTG yang saling terhubung.
SISTEM TINGGI
Secara umum, sistem tinggi dapat digolongkan memjadi dua jenis, yaitu: sistem tinggi geometris dan sistem tinggi fisis. Sistem tinggi geometris adalah sistem tinggi yang pengukurannya dilakukan terhadap bidang acuan matematis atau geometris tanpa memperhitungkan aspek fisik.Salah satunya jenis pengukuran tinggi dengan sistem tinggi geometris adalah tinggi geodetic yang diperoleh dari pengukuran dengan GNSS atau GPS.Adapun sistem tinggi fisis adalah sistem tinggi yang pengukurannya terhadap bidang acuan fisis dan memperhitungkan aspek-aspek fisis, misalnya pengukuran tinggi barometris dan tinggi orthometrik. Sistem tinggi fisis dibagi menjadi tiga, yaitu sistem tinggi dinamik, sistemtinggi orthometrik, dan sistem tinggi normal.Sistem tinggi dinamik adalah tinggi yang dihitung dari perbandingan geopotensial suatu titik terhadap gayaberat normal yang
digunakan. Titik-titik yang memiliki geopotensial yang sama memiliki tinggi dinamis yang sama, karena besarnya gayaberat normal akan berlaku di setiap tempat pengukuran (Hofmann-Wellenhof dan Moritz, 2005 dalam Rakapuri, G.,dkk. 2016). Sistem tinggi orthometrik adalah tinggi yang diukur di sepanjang garis unting-unting dari titik di permukaan bumi sampai ke geoid (Hofmann-Wellenhof dan moritz, 2005 dalam Rakapuri, G.,dkk. 2016). Sistem tinggi normal ditemukan oleh Molodenski (1954) dalam Rakapuri, G.,dkk. (2016), dan sifatnya sangat teoritis sehingga tidak pernah dipakai untuk keperluan praktis.Sistem tinggi normal menggunakan bidang telluroid dan quasi geoid dalam mempresentasikan ketinggian.
GEOID
Geoid disebut sebagai model bumi yang mendekati sesungguhnya. Lebih lanjut geoid didefinisikan sebagai bidang equipotensial gayaberat atau bidang nivo yang berimpit dengan permukaan air laut rata-rata (yang tidak terganggu) (Kahar, S.2007). Banyak ahli mengatakan bahwa definisi geoid tersebut hanyalah suatu ilusi saja, karena suatu permukaan laut rata-rata ideal tanpa gangguan itu tidak pernah ada.Banyak sekali factor-faktor yang mempengaruhi permukaan air laut dan factor tersebuat cukup besar, mengingat air laut yang berupa benda cair tentunya tidak mudah bergerak bila ada pengaruh yang kecilpun. Walaupun permukaan air laut yang ideal tidak akan pernah ada, namun tentunya hal itu biasa didekati, yaitu dengan memperhitungkan semua koreksi-koreksi yang harus diberikan kepada permukaan laut tersebuat. Dalam hubungannya air laut rata-rata (MSL), topografi muka laut (sea surface topogrsphy =SST) mempunyai undulasi terhadap MSL sekitar kurang lebih 2 meter Penentuan geoid adalah penentuan penyimpangan geoid atau undulasi geoid (N) dan defleksi vertikal (ξ) terhadap ellipsoid referensi.Jarak geoid terhadap ellipsoid disebut undulasi geoid (N).Nilai undulasi geoid inilah yang ditentukan untuk memodelkan bentuk geoid yang sebenarnya. Nilai dari undulasi geoid tidak sama di semua tempat, hal ini disebabkan ketidak seragaman sebaran densitas massa bumi. Pemodelan geoid bisa dilakukan pengukuran dengan dua metode, metode tersebut adalah metode gravimetrik dan metode geometrik.
Pengukuran percepatan gayaberat di permukaan bumi merupakan salah satu pekerjaan bagi geodesi dan geofisika. Dalam bidang geofisika, data percepatan gayaberat merupakan bahan interpretasi densitas massa di bawah permukaan bumi untuk menentukan jenis, bentuk, dan ukuran dari suatu material geologi (Li dan Gotze.2001). gayaberat adalah salah satu metode dalam geofisika yang pada prinsipnya adalah berdasarkan anomaly gayaberat yang muncul karena adanya variasi rapat massa batuan yang menggambarkan adanya struktur geoligi di bawah permukaan bumi. Adanya variasi rapat massa batuan di suatu tempat dengan tempat lain, akan menimbulkan medan gaya gravitasi yang tidak merata, perbedaan inilah yang terukur di permukaan bumi. Di permukaan bumi nilai percepatan gravitasi bui dipengaruhi oleh limafaktor, yaitu lintang, ketinggian, topografi di sekitar titik pengukuran, interaksi bumu dengan matahari dan bulan (pasang surut), serta perbedaan rapat masa massa batuan di bawah permukaan bumi.
Koreksi ̶ koreksi Gayaberat : Tujuan dari koreksi gayaberat ini adalah untuk mereduksi nilai gayaberat pengamatan pada geoid dan untuk memindahkan massa topografi luar pada geoid dengan menganggap geoid menjadi suatu pembatasan permukaan [Torge, W.2001]. Koreksi-koreksi gayaberat yang dipakai dalam penelitian ini antara lain:
GAYA BERAT
Pengukuran percepatan gayaberat di permukaan bumi merupakan salah satu pekerjaan bagi geodesi dan geofisika. Dalam bidang geofisika, data percepatan gayaberat merupakan bahan interpretasi densitas massa di bawah permukaan bumi untuk menentukan jenis, bentuk, dan ukuran dari suatu material geologi (Li dan Gotze.2001). gayaberat adalah salah satu metode dalam geofisika yang pada prinsipnya adalah berdasarkan anomaly gayaberat yang muncul karena adanya variasi rapat massa batuan yang menggambarkan adanya struktur geoligi di bawah permukaan bumi. Adanya variasi rapat massa batuan di suatu tempat dengan tempat lain, akan menimbulkan medan gaya gravitasi yang tidak merata, perbedaan inilah yang terukur di permukaan bumi. Di permukaan bumi nilai percepatan gravitasi bui dipengaruhi oleh limafaktor, yaitu lintang, ketinggian, topografi di sekitar titik pengukuran, interaksi bumu dengan matahari dan bulan (pasang surut), serta perbedaan rapat masa massa batuan di bawah permukaan bumi.
Koreksi ̶ koreksi Gayaberat : Tujuan dari koreksi gayaberat ini adalah untuk mereduksi nilai gayaberat pengamatan pada geoid dan untuk memindahkan massa topografi luar pada geoid dengan menganggap geoid menjadi suatu pembatasan permukaan [Torge, W.2001]. Koreksi-koreksi gayaberat yang dipakai dalam penelitian ini antara lain:
- Koreksi Apungan (Drift Correction)
Koreksi ini dilakukan untuk menghilangkan kesalahan pembacaan pada alat akibat perpindahan dari suatu titik pengamatan ke titik pengamatan lain. Pada saat dilakukan perpindahan alat akan terjadi goncangan yang mengakibatkan bergesernya pembacaan titik nol pada alat gravimeter. Secara matematis besarnya koreksi drift diberikan pada persamaan berikut :
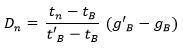
Dimana :
Dn = Koreksi drift pada titik-n
tn = Waktu pembacaan pada titik-n
tB = Waktu pembacaan di titik ikat pada awal looping
t’B = Waktu pembacaan di titik ikat pada akhir looping
gB = Nilai pembacaan di titik ikat pada awal looping
g’B = Nilai pembacaan di titik ikat pada akhir looping
- Koreksi Pasang Surut (Tide Correction)
Koreksi pasang surut bumi dimaksudkan untuk menghilangkan perbedaan pembacaan yang disebabkan oleh pengaruh jarak dari matahari dan bulan pada setiap saat. Pengaruh jarak matahari dan bulan ini akan berpengaruh terhadap bacaan gravimeter. Besarnya koreksi pasang surut [Longman,I.M, 1959], yaitu :
![]()
Dimana :
Tic = Koreksi pasang surut Jurnal Geodesi Undip Agustus 2013 Volume 2, Nomor 3, Tahun 2013, (ISSN : 2337-845X) 93
G = Konstanta gravitasi Newton
M = Massa bulan
r = Jarak titik pengamatan ke pusat bumi
D = Jarak antara pusat bumi dan matahari
d = Jarak antara pusat bumi dan bulan
p = Sudut zenith bulan
q = Sudut zenith matahari
Hasil dari koreksi pasang surut dan koreksi drift kemudian digunakan untuk menghitung nilai gobs dengan persamaan sebagai berikut :
![]()
Dengan gobs adalah gayaberat observasi yang telah dikoreksi drift dan pasang surut
- Koreksi Lintang
Perputaran bumi mengakibatkan perbedaan percepatan gravitasi bumi pada setiap lintang. Oleh sebab itu dilakukan reduksi pada lintang dimana titik observasi berada. Dari proses reduksi ini didapatkan nilai gayaberat normal pada titik yang diamati. Gayaberat normal merupakan suatu nilai teoritis yang mempresentasikan kecepatam gravitasi yang dihasilkan oleh ellipsoidal bumi yang menganggap densitasnya homogen. Dengan memasukkan parameter dari sistem WGS 84 pada persaman gayaberat normal dapat dituliskan sebagai berikut [Torge, W. 2001]:
![]()
Dengan γ0 adalah nilai gayaberat normal pada posisi titik yang diamati dan φ adalah koordinat lintang. Untuk menentukan anomali gayaberat, gayaberat normal yang dipakai harus mengacu pada tinggi ellipsoid permukaan (h). Dalam hubungannya terhadap tinggi ellipsoid persamaan gayaberat normal menjadi :
![]()
- Anomali Gayaberat
Anomali gayaberat adalah perbedaan gayaberat di geoid dan gayaberat normal pada permukaan referensi ellipsoid untuk setiap lintang pengamatan [Heiskanen & Moritz, 1967]. Dalam penentuan geoid lokal atau pada daerah yang dikategorikan dalam permukaan bumi yang datar (flat-earth), nilai anomali gayaberat dan gangguan gayaberat nilainya adalah sama [Sneeuw, N. 2006] :
![]()
Dimana :
∆g = Anomali gayaberat
∂ T = Gangguan potensial
∂ R = Gangguan jarak pusat bumi ke titik pengamatan
Gobs = Gayaberat observasi
Γh = Gayaberat normal terhadap tinggi ellipsoid
δg Gangguan gayaberat
Gangguan gayaberat didefinisikan sebagai selisih antara gayaberat hasil observasi suatu titik gobs di atas permukaan bumi dengan gayaberat normal di titik tersebut γh (pada ketinggian h) :
![]()
Dimana :
Δg = Gangguan gayaberat
gobs = Gayaberat observasi
γh = Gayaberat normal terhadap tinggi ellipsoid
Untuk mendapatkan gayaberat normal (γh) dibutuhkan tinggi terhadap ellipsoid referensi dan dengan menggunakan teknologi GPS, tinggi ellipsoid / geodetik dapat diperoleh dengan mudah melalui persamaan (5).
Perhitungan Undulasi Geoid
Perhitungan undulasi geoid dapat dilakukan dalam berbagai cara dan metode pendekatan salah satunya adalah dengan pendekatan Stokes. Namun untuk perhitungan undulasi geoid dengan Pendekatan Stokes diperlukan informasi gayaberat yang merata di seluruh permukaan bumi (global), sedangkan gayaberat yang tersedia hanya bersifat lokal. Permasalahan ini dapat diatasi dengan menggunakan metode kombinasi yaitu dengan mengkombinasikan antara informasi gayaberat yang bersifat lokal (gelombang pendek) dengan informasi gayaberat yang bersifat global (gelombang panjang). Berikut akan dijelaskan mengenai metode penentuan geoid metode kombinasi.
Metode Kombinasi
Pada prinsipnya pendekatan Stokes adalah perhitungan global, sedangkan data anomali gayaberat hanya tersedia pada daerah yang bersifat lokal. Permasalahan ini dapat teratasi dengan menggunakan metode kombinasi yaitu mengkombinasikan antara informasi gayaberat yang bersifat lokal (gelombang pendek) dengan informasi gayaberat yang bersifat global (gelombang panjang). Formula dasar untuk metode kombinasi diberikan :
N = N1 + N2
Dengan :
N1 = Undulasi geoid dari kontribusi model geopotensial global
N2 = Undulasi geoid dari kontribusi gayaberat lokal dengan Pendekatan Stokes
Kontribusi Model Geopotensial Global (N1)
Kontribusi geoid dari model geopotensial global dihitung menggunakan perpaduan bola harmonik dengan L adalah derajat maksimum model, dengan rumus perhitunganya adalah sebagai berikut :
![]()
Dengan :
N1 = Undulasi geoid dari kontribusi model geopotensial global
R = Jari-jari bola bumi
P̅lm (cos ϑ) = Polinom legendre fully-normalized bola harmonik
ϑ = Co-lintang (90 – φ)
∆C̅lm , ∆S̅lm = Koefisien geopotensial fully-normalized bola harmonik pada model geopotensial global
φ,λ = Koordinat geodetik titik komputasi
l,m = derajat dan orde model geopotensial global
Dalam penentuan kontribusi dari model geopotensial menentukan fungsi legendre fully-normalized bola harmonic P̅lm (cos ϑ) dilakukan dengan beberapa tahapan sebagai berikut [Torge, E. 2001]
1.Menghitung polinom legendre zona harmonik Pl(t)
![]()
2.Menghitung fungsi legendre associated Pl(t)
![]()
3.Menghitung fungsi legendre fully-normalized bola harmonic P̅lm (cos ϑ)
![]()
Kontribusi Gayaberat Lokal (N2)
Perhitungan Kontribusi gayaberat lokal dilakukan dengan pendekatan Stokes. Untuk parameter anomali gayaberat dihitung 2 kali. Pertama-tama kita tentukan terlebih dahulu anomali gayaberat yang sesuai dengan N1. Kemudian kita hilangkan pengaruh anomali gayaberat yang bersifat global tersebut terhadap anomali gayaberat yang bersifat lokal. Tahapan perhitungannya adalah sebagai berikut :
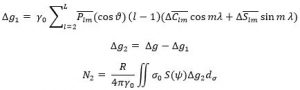
Dimana :
N2 = Undulasi dari kontribusi model geopotensial global
∆g = Anomali gayaberat hasil ukurangeopotensial global
∆g2 = Anomali gayaberat reduksi
R = Jari-jari bola bumi
P̅lm (cos ϑ) = Fungsi legendre fully-normalized bola harmonik
ϑ = Co-lintang (90 – φ)
∆C̅lm , ∆S̅lm = Koefisien geopotensial fully-normalized bola harmonik pada model geopotensial global
φ,λ = Koordinat geodetik titik komputasi
l,m = derajat dan orde model geopotensial global
γ0 = Gayaberat normal diatas permukaan ellipsoid
S([) = Fungsi Stokes
*Catatan : bahwa daerah integrasi σ0 merupakan batas daerah yang kita ukur anomali gayaberatnya.
Dalam menentukan undulasi geoid dengan pendekatan Stokes digunakan metode Fast Fourier Transform (FFT). FFT mengasumsikan fungsi grid menjadi periode dalam x dan y, grid-grid tersebut harus melingkupi dari daerah pengamatan.
Daftar Pustaka :
Kahar, Sutomo. 2007. Diktat Pelengkap Kuliah Kerangka Dasar Vertikal. Penerbit Teknik Geodesi UNDIP. Semarang
Rastawira, T., Kahar, S., Sabri. 2013. Permodelan GEOID Kota Semarang. Semarang. Teknik Geodesi Universitas Dipoegoro
Rakaputri, G., Sudarso, B., Yuwono, BD. 2016. Permodelan GEOID Lokal Universitas Diponegoro. Semarang. Teknik Geodesi Universitas Dipoegoro
Heiskanen, Weikko A. Dan Helmut Moritz. 1967. Physical Geodesy. United State of America : W.H. Freeman and Company.
Longman, I.M. 1959. Formulas for Computing the Tidal Acceleration due to the Moon and the sun. J. Geophys. Res., 64,2351-2355.
Sneeuw, Nico. 2006. Lecture Notes : Physical Geodesy. Stuttgart : Institute of Geodesy Universitat Stuttgart.
Torge, Wolfgang. 2001. Geodesy, 3rd Edition. Berlin : De Gruyter
DAFTAR SEKARANG!!
Training Center di Yogyakarta
Contact us
1. Dwi Purwanto
085602006858 (m3)
081328361414 (simpati)
Email: fetc.trainingcenter@gmail.com
admin@frastatraining.com
2. Kurnia
08179414410 (xl)
Email: kurniafrasta@gmail.com
FETC,Ruko house of Tajem no A 1 JL Raya Tajem km 2 Panjen Wedomartani Ngemplak Sleman Yogyakarta,
Telp 0274 4462970
OUR SOCIAL MEDIA
mau lanjut WA langsung??
Materi Selengkapnya Click Di Sini
Informasi Pelatihan Selengkapnya Click Di Sini
#pelatihandroneuntukpemetaan
#pelatihandronemapping
#pelatihandrone
#PelatihanPemetaanDrone
#PelatihanDroneJakarta
#PelatihanDroneJogja
#PelatihanDrone2022
#ModulPelatihanDrone
#DronePemetaanWilayah
#PelatihanPemetaan
#pelatihanuav
#pelatihan
#trainingdrone
#pelatihandrone
#trainingyogyakarta
#campussurveying
#trainingpemetaanuav
#pelatihanpemetaanindonesia
#SurveyorIndonesia
#surveying #mining #surveyor #fetc
#training #pelatihan #belajargps
#belajaruav #belajarsurvey
#pertambangan #surveyortambang
#juruukur #trainingpemetaanindonesia
#pelatihansurveydanpemetaan
#pelatihanpemetaan
#kursussurveydanpemetaan
#materisurveypemetaan
#pelatihanjuruukursurveypemetaan
#surveypemetaan
#geolistrik
#geolistrikonline
#pelatihangeolistrik
#pelatihangeolistrikonline
#geofisika
#mencariairtanah


